Der Himmel über La Palma, von Klaus Fuhrmann

Im Licht der Sterne lesen - Teil IV

Sie werden das kennen: man steht an der Straße und möchte auf die andere Seite, doch ein Krankenwagen nähert sich mit lauten und hellen Signaltönen. In dem Moment, als er Sie passiert werden diese merklich tiefer. Man macht diese Beobachtung auch bei Automobil-Rennen, oder mit vorbeifahrenden Zügen. In der Physik wird das hier zu beobachtende Phänomen als Doppler-Effekt bezeichnet, nach Christian Doppler, der diesen im Jahre 1842 als erster entdeckte. Entscheidend für die Erklärung dieses Effekts ist die relative Bewegung zwischen Krankenwagen und Beobachter, und der Ton der Sirene sozusagen das Indiz dafür. Stellen Sie sich im Folgenden der Einfachheit halber vor, der Krankenwagen hätte keine Sirene, sondern würde alle drei Sekunden eine Brieftaube aus einer Öffnung frei lassen, die ihrerseits sofort versuchen würden, uns als Beobachter am Straßenrand zu erreichen. (Außerdem sei angenommen, daß alle Brieftauben gleichschnell fliegen.) Eine Brieftaube nach der anderen gelangt so zu uns, auch wenn wir den Krankenwagen zunächst weder sehen noch hören. Schließlich kommt er dann aber doch, fährt an uns vorbei, und wir erkennen vielleicht noch auf die Schnelle, wie die eine oder andere Brieftaube abgeschickt wird. Dann ist der Krankenwagen aber auch schon wieder weg.

Nur die weiterhin bei uns eintreffenden Brieftauben geben uns von ihm Kunde. Doch jetzt bemerken wir einen Unterschied: nachdem uns der Krankenwagen passiert hat, dauert es immer etwas länger bis die nächste Brieftaube uns erreicht. Man könnte nun meinen, daß das jetzt mit dem weiten Weg zusammenhängt, den die Brieftauben nun zurücklegen müssen. Das aber wäre dann doch zu einfach, denn weite Wege hatten die Brieftauben zu Beginn auch zurückzulegen. Entscheidend ist hingegen, daß jede nunmehr bei uns eintreffende Brieftaube relativ zu ihrer unmittelbaren Vorgängerin einen weiteren Weg hat. Nicht der Weg an sich, sondern die Differenz, beziehungsweise der daraus folgende Takt mit dem die Brieftauben nun eintreffen, ist entscheidend.

Nach einer bestimmten Dauer, deren Länge sich in dem Moment ändert, als der Krankenwagen uns passiert, trifft also eine Brieftaube nach der anderen bei uns ein. Als "Botenteilchen" könnten wir den Brieftauben nun eine bestimmte Taktzahl und sogar eine bestimmte "Wellenlänge" zuordnen, wobei letztere sich aus dem zwischen zwei Brieftauben liegenden Weg ergibt.

Im Gegensatz hierzu kommt der Signalton des Krankenwagens als Informationsträger natürlich nicht mit "Brieftaubengeschwindigkeit" daher, sondern mit Schallgeschwindigkeit. Solange der Krankenwagen sich uns nähert haben die Schallwellen jetzt eine geringere Wellenlänge, beziehungsweise eine höhere Taktzahl oder "Frequenz" - wie man sagt. Hat der Krankenwagen uns passiert, wird die Taktzahl geringer, die Schallwellenlänge aber entsprechend größer. Diese längeren Schallwellen nimmt das menschliche Ohr nun als tieferen Ton wahr (und entsprechend die kurzen Wellen als hohen Ton).

Und was für die Schallwellen gilt, ist ähnlich auch für das Licht anwendbar. Wir hatten im letzten Monat bereits von den Lichtteilchen - den "Photonen" gesprochen. Man kann sich das Licht aber auch als Wellenvorgang vorstellen, und die Photonen gleichsam als Wellenpakete mit einer dazugehörigen Lichtwellenlänge und Frequenz.

Bewegt sich eine Lichtquelle - zum Beispiel ein Stern - in unsere Richtung, so wird die Lichtwellenlänge etwas verkürzt. Das kurzwelligere Licht ist aber etwas energiereicher, und somit zum ultravioletten Licht hin verschoben. Andererseits, entfernt sich der Stern, erhalten wir eine Doppler-Verschiebung zu langwelligerem Licht, also in Richtung der infraroten Strahlung.

Um Ihnen ein drastisches Beispiel zu geben: wenn man mit 50 km/h auf eine rote Ampel zufährt, präsentiert diese sich mit praktisch dem gleichen Rot, das auch ein Fußgänger sieht. Fährt man aber mit etwa 46000 km/s (wohlgemerkt: Kilometer pro Sekunde!) auf eine rote Ampel zu, sieht man auf Grund des Doppler-Effekts deren Licht deutlich kurzwelliger, nämlich grün! Physikalisch gesehen fährt man dann also völlig korrekt "bei Grün" über die Ampel. (Den Führerschein wird man aber wahrscheinlich dennoch los, wegen der wesentlich zu hohen Geschwindigkeit nämlich, wobei sich allerdings auch die Frage stellt, wer einen bei dieser überhaupt noch stoppen kann.)

Da nun aber alle Sterne der Milchstraße relativ zu uns, wie auch untereinander, in Bewegung sind, ist deren Licht auch immer etwas zum kurzwelligen oder langwelligen - oder, wie die Astronomen sagen, zum "Blauen" oder zum "Roten" - hin verschoben. Die Geschwindigkeiten, um die es hier geht, sind nun nicht die aus dem eben erwähnten Beispiel mit der roten Ampel. Die Sterne in unserer Nachbarschaft bewegen sich typischerweise "nur" mit einigen Kilometern pro Sekunde relativ zu uns. Schauen wir aber mit großen Teleskopen die sehr weit entfernt stehenden Galaxien an, so werden auch 46000 km/s mühelos erreicht. (Interessanterweise sind alle Galaxien aber nur ins Rote verschoben, wie wenn sie nichts mit uns Erdenbewohnern zu tun haben möchten, aber darüber unterhalten wir uns ein anderes Mal.)
Jetzt kommen wir noch einmal auf die Abbildung 2 vom Vormonat zu sprechen und fragen uns: Was passiert eigentlich mit den Spektrallinien in den Spektren der Sterne, wenn letztere sich auf uns zu, oder von uns weg bewegen? Jede Spektrallinie repräsentiert eine bestimmte Energie, beziehungsweise Wellenlänge des Lichts. Bei einer relativen Bewegung eines Sterns auf uns zu oder von uns weg, beginnen nun auch die Spektrallinien zu wandern. Das sieht man zwar nicht in Abbildung 2 vom Vormonat (Feb-2007), da hier die Spektren alle Sterne zur Deckung gebracht wurden. Man erkennt es aber in Abbildung 1 für die Sonne und den uns sehr nahen, sonnenähnlichen Nachbarstern "Tau Ceti", dessen beider Spektrallinien deutlich gegeneinander verschoben sind. Die genaue Messung ergibt hier eine relative Geschwindigkeit - eine "Radialgeschwindigkeit", wie man sagt - von 16.6 km/s, das heißt Tau Ceti bewegt sich mit 16.6 km/s auf uns zu. Das sind also etwa 60000 Kilometer pro Stunde, oder mehr als eine Millionen Kilometer pro Tag.

Abbildung 1: Ausschnitt aus dem Spektrum der Sonne und dem sehr nahen, sonnenähnlichen Stern "Tau Ceti", der bereits mit bloßem Auge am Nachthimmel über La Palma gut zu erkennen ist. Da sich Tau Ceti auf uns zu bewegt - und zwar mit 16.6 km/s (also etwa 60000 km/h) - sind seine Spektrallinien deutlich nach links zum energiereicheren, kurzwelligeren blauen Licht verschoben.

Ein anderes Beispiel zeigt Abbildung 2. Hier entfernt sich der Stern "Mu Virginis" von uns, bzw. der Sonne, mit 5.2 km/s (also etwa 19000 km/h). Die Spektrallinien liegen daher etwas nach rechts verschoben. Allerdings fällt auch auf, daß diese jetzt sehr breit und verwaschen sind.

Abbildung 2: Wie Abbildung 2, jetzt allerdings für den Stern "Mu Virginis", der sich im Gegensatz zu Tau Ceti von uns weg bewegt. Besonders auffällig sind zudem die sehr breiten, verwaschenen Linien von Mu Virginis.

Um das nun näher zu untersuchen, werden beide Spektren zunächst unter einen Scanner gelegt (wie man ihn ähnlich auch bei vielen Photokopierern findet) und von diesem sodann eingelesen. Abbildung 3 zeigt das Ergebnis für das Sonnenspektrum. Die dunklen Spektrallinien, also die Bereiche mit geringem Licht, haben auch nur eine geringe Intensität.

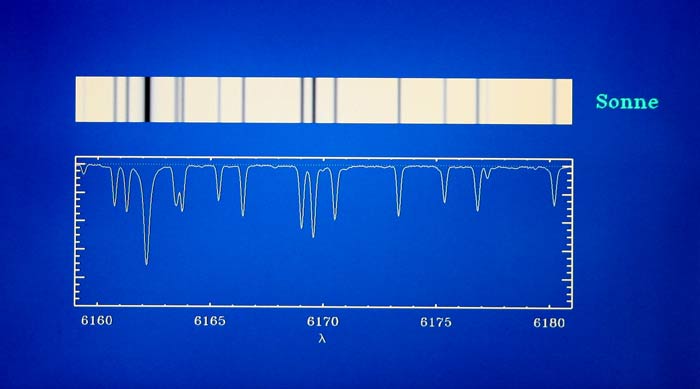
Abbildung 3: Ausschnitt aus dem Spektrum der Sonne (oben) und das Ergebnis, wie es von einem Scanner produziert wird (unten). Letzterer tastet sozusagen das Spektrum der Sonne von links nach rechts ab. In der jetzt vorliegenden Form des Spektrums erkennt man die Profile der Spektrallinien besonders gut. So manches Detail, das der Stern in den Profilen seiner Spektrallinien versteckt hält, läßt sich auf diese Art besonders gut untersuchen. Die darunter angeschriebenen Zahlen bedeuten übrigens die genauen Lichtwellenlängen, welche die Astrophysiker bevorzugt mit dem griechischen Buchstaben "lambda" abkürzen.

Jetzt lesen wir das Spektrum von Mu Virginis in gleicher Weise ein und stellen es dem der Sonne in Abbildung 4 gegenüber. Man erkennt: das hier mit der Farbe lila gezeichnete Spektrum von Mu Virginis hat wesentlich breitere Linien als die Sonne. Ahnen Sie aber auch schon, womit das vielleicht zusammenhängen könnte?

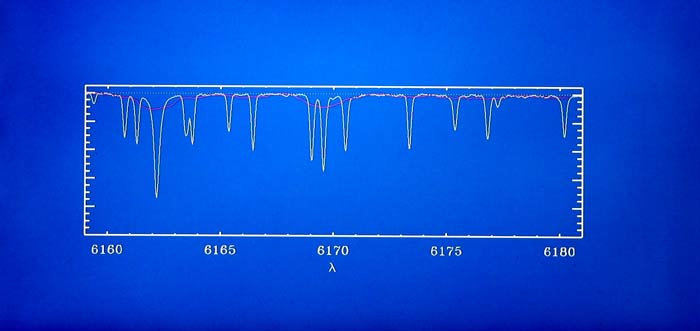
Abbildung 4: Ausschnitte aus den Spektren der Sonne (weiß) und Mu Virginis (lila). Die Linien von Mu Virginis sind deutlich breiter oder "verwaschener". Der Grund hierfür ist in der höheren Drehgeschwindigkeit von Mu Virginis zu finden: während die Sonne mit nur 2 km/s um die eigene Achse rotiert, erhält man für Mu Virginis immerhin 46 km/s.

Die Antwort findet sich in der Rotation, also der Drehung des Sterns um seine eigene Achse. So wie die Erde sich um die eigene Achse dreht und damit für den Wechsel von Tag und Nacht sorgt, erkennt man auch bei der Sonne, z.B. aus der Beobachtung ihrer Sonnenflecken, eine Drehbewegung. Die Erde braucht für eine Drehung nur knapp 24 Stunden, die Sonne etwa einen Monat. Es gibt aber auch Sterne, die drehen sich in nur wenigen Stunden um die eigene Achse.

Wenn ein Licht aussendender Stern sich nun aber um seine eigene Achse dreht, so haben die verschiedene Bereiche seiner Oberfläche relativ zu uns auch unterschiedliche Geschwindigkeiten, die vor allem am Rand merklich werden. Die Sonne dreht sich zum Beispiel mit etwa 2 Kilometer pro Sekunde um die eigene Achse. Das Licht beider Randbereiche hat dann also eine relative Geschwindigkeit von 2+2=4 Kilometer pro Sekunde: während der eine Rand mit 2 Kilometer pro Sekunde von uns wegweicht, kommt der gegenüberliegende Rand mit genau dieser Geschwindigkeit auf uns zu. Ein Teil des Sonnenlichts wird so also nach links zum Blauen, der andere Teil nach rechts ins Rote verschoben. Der Schwerpunkt der Sonne bewegt sich natürlich nicht auf die Erde hin oder von ihr weg, denn wir beschreiben ja praktisch eine Kreisbahn um unseren Heimatstern. Wenn die Sonne sich nun aber relativ zu uns praktisch in Ruhe befindet und lediglich auf Grund ihrer Eigenrotation das Licht in unterschiedliche Richtungen "in Bewegung" versetzt was ist dann der Effekt? Genau der, den wir in Abbildung 4 erkennen: die Spektrallinien verbreitern sich.
Würde sich die Sonne also nicht auch in Rotation befinden, wären ihre Spektrallinien noch schärfer. Andererseits, sind die Linien der Sonne im Vergleich zu Mu Virginis bereits als "messerscharf" anzusehen.

Wir erkennen also im Prinzip die Eigenrotation eines Sterns an der Breite seiner Spektrallinien. Da zum Beispiel viele junge Sterne eine hohe Eigenrotation besitzen, kann man bereits auf diese Art erste wichtige Informationen über die Natur eines Sterns erhalten. Eine Schwierigkeit besteht allerdings darin, daß wir manche Sterne genau "von oben" sehen - dann wird der Doppler-Effekt naturgemäß nicht wirksam. Daher können auch Sterne mit scharfen Spektrallinien in Wirklichkeit sehr schnell rotieren.

Neben der Rotation eines Sterns, kann seine Bewegung auf uns zu oder von uns weg, die "Radialgeschwindigkeit", an der Doppler-Verschiebung der Spektrallinien - so wie in Abbildung 1 gezeigt - erkannt werden. Zusammen mit der so genannten "Eigenbewegung" der Sterne (siehe Sep-2006), welche die Veränderung am Himmel in Längen- und Breitengraden beschreibt, gestattet die zusätzliche Messung der Radialgeschwindigkeit also die vollständige 3-dimensionale Raumbewegung der Sterne abzuleiten. Mit dem Doppler-Effekt haben wir damit ein zentrales Werkzeug der Astrophysik kennen gelernt.
Die Diagnostik der Spektrallinien ist damit aber keineswegs bereits erschöpft. Wir kennen jetzt gerade einmal einige wichtige Beispiele, sozusagen die Spitze des "Spektroskopie-Eisbergs", der den Astrophysikern schon ungezählte Erkenntnisse geliefert hat.

Wie es so im Jahre 1995 erstmals möglich wurde die Existenz extra-solarer Planeten - also Planeten a u ß e r h a l b unseres Sonnensystems - mit Hilfe der Spektroskopie nachzuweisen, erfahren wir im nächsten Monat.